In a convolutional neural network, convolutional layers learn hiearchical features. The lower layers learn low-level features like edges, corners, etc. and higher layers high level features like mouth, ears, tail,etc. Increasing the network depth, as demonstrated by InceptionNet, allows the network to learn better representations and improves the performance of the network. However, optimizing such deep networks is not that easy.

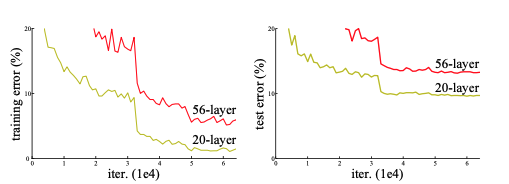
The graph above compares a 56-layered network with a 26-layered network. The error is higher for deeper network in both cases leading to a lower accuracy. This drop in accuray is not due to overfitting because the deeper network is performing poorly in both the training and test data. In fact, this poor performance of the deeper network is due to the degradation problem. As the deeper network start converging, accuracy gets saturated and eventually degrades rapidly.

This degradation problem indicates that not all networks are easy to optimize. To corroborate this, let us consider two networks:

• a shallower network, and
• its deeper counterpart with few additional layer

If we train the shallow network, copy its weight to the canonical layers of deeper network and the additional layers of the deeper network are just identity mapping, the deeper network should produce no higher training error than the shallower one. But experimental results show that the deeper network with multiple non-linear layers is unable to learn such identity mapping(or unable to do so in feasible time) and get results as good as or better than the shallower network.

To tackle the degradition problem, the author of ResNet propose a deep residual learning framework. Instead of assuming that a few group of layers learn the underlying mapping, we explicitly let the layers learn residual mapping. If \(\mathcal{H}(\textbf{x})\) is the underlying mapping to be learned, the network is trained to learn residual mapping of \(\mathcal{F}(\textbf{x}) := \mathcal{H(\textbf{x})}- \textbf{x}\). We then explicitly add \(\textbf{x}\) to the learned \(\mathcal{F}(\textbf{x})\). The figure below elucidates this.

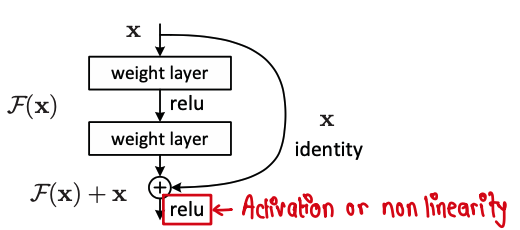
It is important to note that we apply relu activation after we add \(\textbf{x}\) to \(\mathcal{F}(\textbf{x})\) and the identity mapping or the shortcut connection don’t add any extra parameters or computational complexity.

The residual mappings are much convenient to optimize than the original unreferenced mapping. If the identity mapping were optimal, then it is easier for the network to simply push the weights corresponding to the residual to zero instead of fitting an identity mapping using nonlinear layers.

But, in case of a neural networks, is an identity mapping the optimal function?. The answer is no, identity mapping is not the optimal function. However, experiments show that, in case of residual networks, the layer response is close to zero indicating that the optimal function is very close to the identity mapping and is obtained my making minor adjustments to the identity mapping.

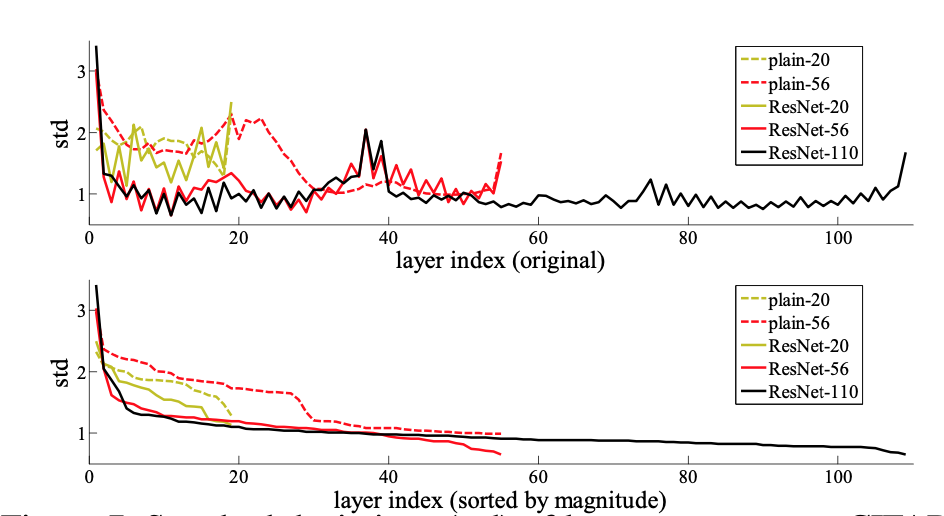
The above figure compares the layer response of residual network with non-residual counterparts. The bottom figure represents the layers response arragned in descending order. Layer response for residual networks is low and close to zero compared to the plain networks. The response is even lower in case of deeper residual networks.

Hence, since the optimal function is close to the identity mapping, residual units help to the network converge faster and make the deep network easier to optimize.

References

1. Going Deeper with Convolutions, Szegedy et. al.

2. Deep Residual Learning for Image Recognition, He et. al.